编程与数学(五):Trailing zeroes in factorial
1/13/2019
缘起
最近在看《编程之美》,里面有一小节是探讨 N! 的阶乘的尾部零的数量的问题。里面提出来一个规律即对于 N! 的二进制表示,则尾部的零的数量为 N - one_bits(N),即 N 减去 N 的二进制表示里 1 的数量,只需要 O(1) 的时间即可求解该问题。然后书里面举了一个例子,但是没有给出证明为什么这个规律成立。这么优雅的规律怎么能没有证明呢,它真的成立吗?
Why?
首先书里面指出 binary(N!) 尾部零的数量 = N / 2 + N / 4 + N / 8 .... 直到 N / (2^k) 为 0 为止,这个很容易理解,接下来比较关键的就是证明 N / 2 + N / 4 + N / 8 .... 直到 N / (2^k) 为 0 为什么等于 N - one_bits(N)。(这里的 / 是 C 里面的 / )
下面给出证明,如有错误欢迎指出:
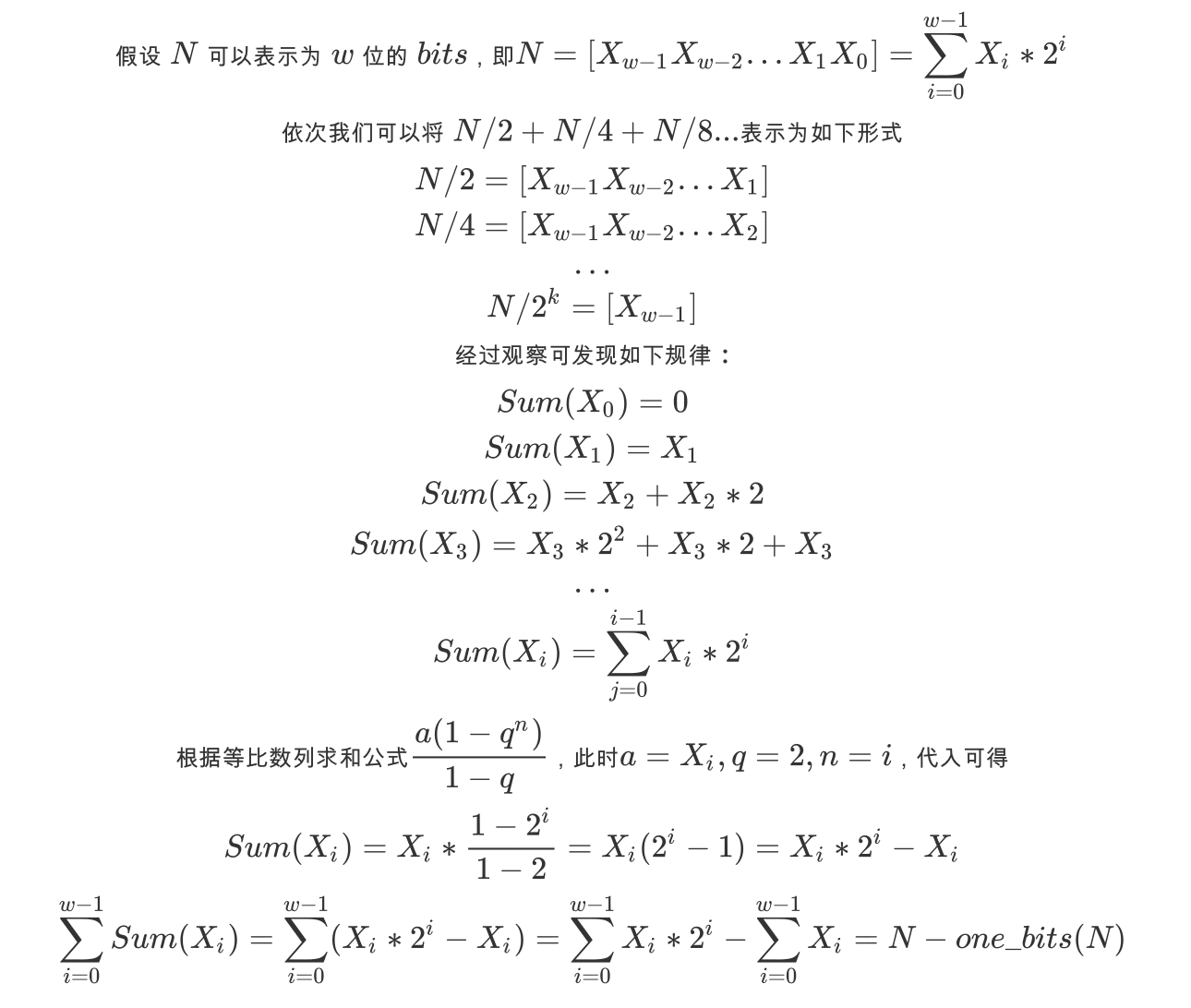
结尾
优雅的结论背后一定隐藏着优雅的证明,我想这就是数学猜想的魅力所在吧!