跑步与数学

缘起

最近有一天晨跑的时候，突然想到了刚学的微积分里面的 The Mean Value Theorm。因为记得书上说这是微积分中最重要的定理之一，就心血来潮想回忆下这个定理是怎么推导出来的？也因此有了一段很奇妙的体验。

正文

The Mean Value Theorm 简述如下:

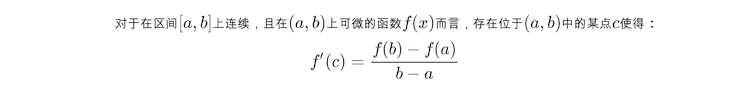
证明如下:

而此时我们可以回想起 Rolle's Theorem:

代入上式，则

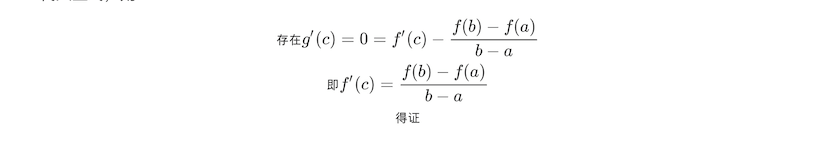
这里不由得要问，为什么Rolle‘s Theorm成立呢？证明简述如下：

那为什么当 f(x) 不为常量时它的极值导数一定为 0 呢？

尾声

这时候我没有疑问了，心满意足了，而跑步也临近结束，此时我内心的满足感无以复加，仿佛一个小孩终于得到了自己想要的东西。

那这些数学的推论跟跑步有什么关系呢？因为只有在跑步的时候才能放空自我，让思维漫无边际的漫游，飘荡在这世界中，欣赏人类纯粹的智慧成就。

我突然理解为什么那么多人醉心于数学的优雅和精致。在现实生活中，有很多问题你无法获得解答，但是在数学中，对于你感到疑惑的定理，只要你有好奇心，你总是可以问到你心满意足为止。

我想，这是不是所谓的苏格拉底式提问法呢？一直追问下去，直到你的好奇心满足或者回答不了发现自己的盲点为止。

最近我偶然看到了一个费曼关于 why 的视频，里面也谈到了类似的思考方式。我想用一句话总结我的感受:

Ask why! Ask why! Ask why until you're satisfied!