编程与数学(三)：Newton‘s Method

缘起

前几天看到一道题目，是关于“对整数 n 开平方，求其整数部分”，解法用到了 Newton's Method，因为之前刚刚学过，就顺便复习下什么是 Newton's Method，为什么可以用于求解这道题?

Newton's Method

本身是用于逼近函数零点的一种技巧。因为对没有求根公式的函数，求解它的零点是非常困难的，因此就发明了 Newton‘s Method 来逼近该函数的零点。具体方法如下图所示:

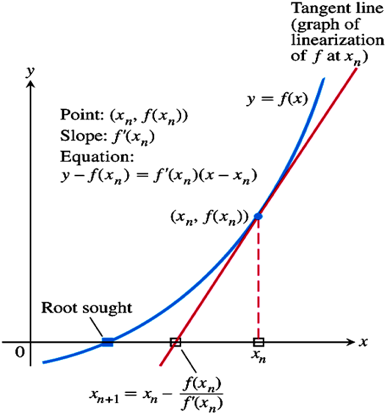
应用

至于为什么用于逼近函数零点的 Newton's Method 会跟 “对整数 n 开平方” 有关 代码实现如下:

def int_sqrt(n):
    """
    >>> int_sqrt(0)
    0
    >>> int_sqrt(1)
    1
    >>> int_sqrt(80)
    8
    >>> int_sqrt(81)
    9
    >>> int_sqrt(82)
    9
    """
    x_n = 1 
    x_n_plus_1 = (1 + n) / 2
    #while int(x_n_plus_1) != int(x_n): 原来的错误做法，具体见评论
    while abs(x_n_plus_1) != int(x_n):
        x_n = x_n_plus_1
        x_n_plus_1 = (x_n + n / x_n) / 2
    return int(x_n_plus_1)

如果是开 k 次方呢？

代码实现如下：

def int_sqrt_of(n, k=3):
    """
    >>> int_sqrt_of(26, 3)
    2
    >>> int_sqrt_of(27, 3)
    3
    >>> int_sqrt_of(28, 3)
    3
    """
    x_n = 1
    x_n_plus_1 = (k - 1 + n) / k
    while abs(x_n_plus_1 - x_n) > 0.01:
        x_n = x_n_plus_1
        x_n_plus_1 = ((k - 1) * x_n + n / x_n ** (k - 1)) / k
    return int(x_n_plus_1)