编程与数学(一)：Logistic Differential Equation

最近在准备尝试复活我很久前写的网文推荐系统，把 2 年前推送到 daocloud 的 Docker 镜像重现部署到了现在新的服务器，并暂时放到了这个域名。

这时候发现一个问题，里面的相似度计算是基于余弦算法，一般同作者的两本书 A、B 之间的相似度在 30% ～ 35% 左右，位于 35% 到 100% 间的极少，而 20% 左右已经不太像了。这时候就想找一个 mapping 算法，希望能满足以下特征：

• 结果值随着原始相似度的提高剧烈上升，在 30% 时候能映射到 90% 的相似度

• 结果值最大为 100%，因为最多就 100% 相似

• 在 20% 相似度左右的时候结果值较低

理想中应该是个 S 型的曲线。根据第一个特征想到了基于指数增长的函数:

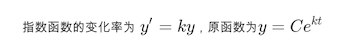
但是它不满足有极大值的限制，这时候就想到了常用于描述人口增长的 Logistic Differential Equation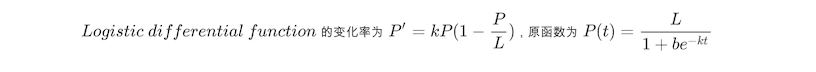： 完美满足了前期指数级上升，又存在一个极限 L 的情况。但是它也有一个不太完美的地方，就是当相似度为 0 时它的值不能为 0 ， 所以只能假设相似度为 0 时方程值为 1。

接下来就是解方程获取精确的公式了：

求解后就是试着画图和输入 0 到 100 之间的数值感觉符不符合预期了，结果如下 ，图中灰线交点为(30, 90):

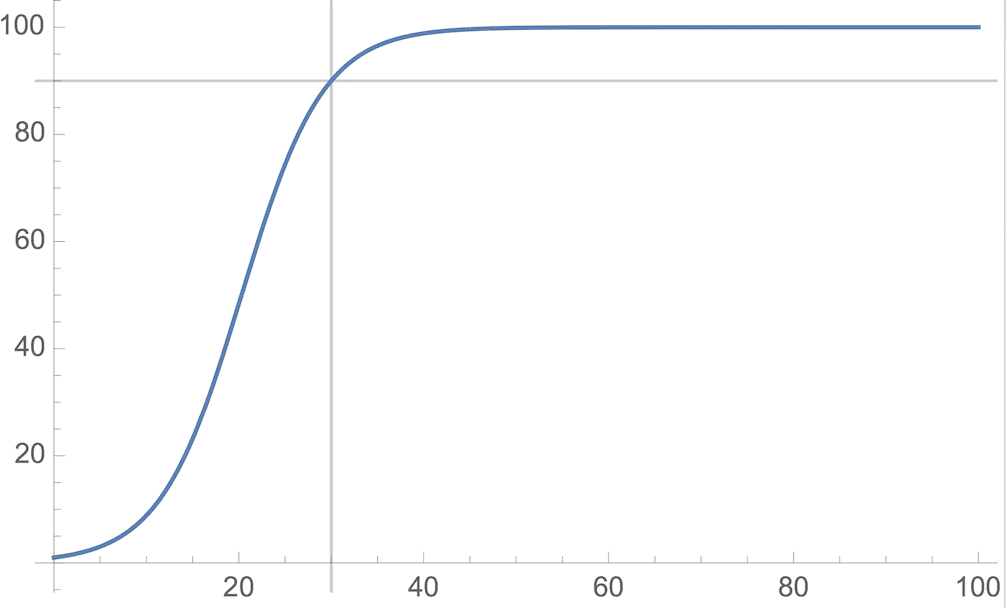
精确值如下：

0      1.00000
5      3.03817
10     8.85875
15    23.16620
20    48.32840
25    74.36770
30    90.00000
35    96.54200
40    98.85850
45    99.62910
50    99.88010
55    99.96130
60    99.98750
65    99.99600
70    99.99870
75    99.99960
80    99.99990
85   100.00000
90   100.00000
95   100.00000
100  100.00000

感觉还不错，参数可能还需要根据实际情况微调。如果有更好的 mapping 函数或者方法，欢迎大家留言。