编程与数学(二)：Geometric Series

编程与数学(2): Geometric Series

缘起

前几天偶然看到一道题：A、B 打赌互相扔硬币，先抛出正面的人胜利，假设 A 先抛的话他赢的概率是多少？ 当时跟同事讨论了下，结果是 2/3。感觉这题挺有意思的，就想详细研究下，所以有了这篇文章。

解法

从概率的角度看，第一个人可能赢在第 1、3、5、7 ..... 次，而每次赢必然是前几次抛硬币结果都为负，最后一次为正，因为抛硬币为独立事件，则可以知道赢的概率之和为:

还有呢？

如果有 3 个人或者说 k 个人打赌，那第一个人赢的概率是多少呢？

如果是 3 个人打赌，则第一个人可能赢在第 1、4、7、11 ..... 次，则在级数中对应的项次由两个人时的 2n+1变为 3n+1(注:n 从零开始)，同理可得如果是 k 个人，则为 kn+1，则可以知道 k 个人时赢的概率之和为：

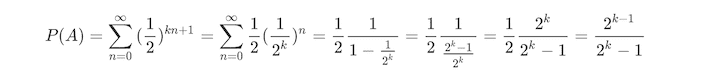
令 k=3，则 P(A) = 4 / 7。

如果 A、B 决定加点难度，改为掷骰子，先掷出 6 点的人胜，那第一个人赢的概率是多少呢？

同理可知，第一个人可能赢在第 1、3、5、7 ..... 2n+1 次，稍微不同是赢之前的那几次，他们只需要不掷出 6 即可:

如果是掷 t 面骰子，先掷出 t 点的人赢，那第一个人赢的概率是多少？

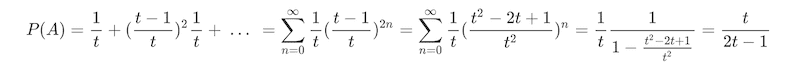
如果是 k 个人掷 t 面骰子，先掷出 t 点的人赢呢，那第一个人赢的概率是多少？

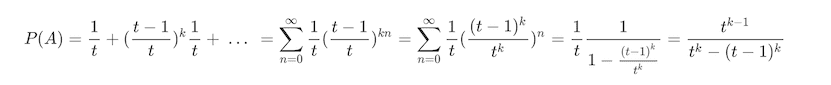
结尾

从上可以知道其实所有变化都只是 Geometric Series 的变种。这就是数学的魅力所在，从各种各样的形式中发现统一的模式，又将这统一的模式应用于无穷无尽的变化中。

枢始得其环中，以应无穷。 --《庄子·齐物论》