记一次业务中的算法应用：动态规划、图、树

缘起

我的编程知识大部分都是自学的，算法并不好。但是作为程序员的自尊心告诉我，算法很重要，所以后面看了《Data Structures and Algorithm Analysis in C:Second Edition》、《Algorithms》这几本书入门了算法。

非常幸运的是这两本书都有国内的英文版，价格低廉，尤其《Data Structures and Algorithm Analysis in C》售价仅仅 30 元。

简洁优雅的算法搭配精妙绝伦的数据结构，时常给人以一种美的享受。

但是在业务中，算法的应用并不多，就算遇到了，通常也有了比较好的封装。但是之前我曾遇到一个问题，就很巧的利用了我学到的算法知识，最后也取得了不错的效果。

翻译模块的优化

不久前公司准备优化性能，经过分析发现翻译模块的性能差强人意，所以准备从这个地方入手，而我正好被分配来处理这个问题。下面是这个问题的简化版本：

翻译模块的功能

翻译模块是将数据库表的字段在展示给用户时进行翻译。假设有如下表结构（表名、字段右侧为对应翻译，表结构纯为示例）：

user: 用户

• name: 姓名
• father: Foreign Key of 「user」: 父亲，也是指向自己的一个外键

car: 汽车

• brand: 品牌

• owner: Foreign Key of 「user」: 拥有者，也是指向 「user」表的外键

翻译模块的接口函数 translate 需要实现的功能为(省略无关细节)：

• 输入表名、字段名，根据预设翻译输出对应的翻译数组，最后通过指定分隔符连接，比如中文用”的“。

  • user, name => 用户, 姓名 => 用户的姓名
  • car, brand => 汽车, 品牌 => 汽车的品牌

• 支持外键无限级联扩展，包括反向。

  • user, father, name => 用户, 父亲, 姓名 => 用户的父亲的姓名
  • user, car, brand => 用户, 汽车, 品牌 => 用户的汽车的品牌

• 支持循环引用

  • car, owner, father, father, name => 汽车, 拥有者, 父亲, 父亲, 姓名 => 汽车的拥有者的父亲的父亲的姓名

• 支持自定义翻译

  • 从上一个示例可以看出，字段过多时直接翻译会导致结果过长，影响用户体验，而实际预设最长有近 20 个字段，同时用户可以自定义字段，实际长度更长。
  • 这个问题可以通过引入自定义翻译缓解。如果预先自定义翻译 [car, owner] => ”车辆所有人"，[father, father] => ”爷爷"，则 [car, owner, father, father, name] => 车辆所有人的爷爷的姓名，相比原来简短很多。

• 其他

  • 通用翻译的共享
  • 多语言、增删改查等本文无关细节

因为翻译一部分来源是机器翻译，字段有数十万而且请求频率非常高，所以对翻译速度和内存有一定要求。

自定义翻译的实现

简单分析后发现这是一个算法问题，问题描述如下：

翻译模块之算法

给定两个字符串数组 arr1 以及 arr 2，arr1 为待翻译数组，arr2 为自定义翻译数组。待翻译数组中的字符可用自定义翻译中的匹配字符串替代，给出使得翻译结果片段最少的输出结果，有多个时输出任一即可。示例如下：

给出 arr1 = A, B, C, D, E, F，arr2 = B-C，C-D-E, E-F-G

• 输入 [A, B]，因为 arr2 无匹配，输出 [A, B]，最少为 2。

• 输入[A, B, C]，arr2 中的 [B-C] 可取代匹配子数组 [B-C]，输出 [A, B-C]，最少为 2。

• 输入 [A, B, C, D, E]，用 [C-D-E] 取代比使用 [B-C] 取代更短，所以输出 [A, B, C-D-E]，最少为 2。

• 输入 [B, C, D, E, F, G]，用 [B-C, E-F-G] 取代比使用 [C-D-E] 取代更短，所以输出 [B-C, D, E-F-G]，最少为 3。

解法

典型的动态规划，对应方程为：

F_min(i) = min(F_min(i - 1) + 1, F_min(j) + 1) (j 满足 arr1[j + 1],...,arr[i] 的片段在 arr2 中存在)

• F_min(i) 指 arr1 到 i 下标为止时满足条件的最少片段数
• F_min(j) + 1 是指如果存在满足 arr1[j + 1: i + 1]的可替代片段存在于 arr2，即可以基于此加 1
• 时间复杂度 O(N^2)

比如翻译如上的 A, B, C ，初始条件 F_min(-1) = 0; F_min(0) = [A] = 1

• i = 1, F_min(1) = min(F_min(0) + 1, F_min(j) + 1)，因为 arr2 中不存在 A-B，所以 j 不存在，F_min(1) = F_min(0) + 1 = 2
• i = 2, F_min(2) = min(F_min(1) + 1, F_min(j) + 1)，此时存在 j = 0 时，arr1[1 : 3] = [B, C] 的片段 B-C 在 arr2 中存在，所以 F_min(2) = min(F_min(1) + 1, F_min(0) + 1) = min(2 + 1, 1 + 1) = 2

最少片段数为 2，实际的翻译结果为 A, B-C

代码

完整见 Github

def find(fields, seqs):
    cost = [0] * (len(fields) + 1)
    path = [None] * len(fields)
    for i in range(len(fields)):
        cost[i] = cost[i - 1] + 1
        for j in range(i - 1, -1, -1):
            if tuple(fields[j: i + 1]) not in seqs:
                continue
            if cost[j - 1] + 1 < cost[i]:
                cost[i] = cost[j - 1] + 1
                path[i] = j
    return cost, path
  
fields = ('A', 'B', 'C', 'D', 'E', 'F')
custom = {
        ('A', 'B'),
        ('B', 'C'),
        ('C', 'D', 'E'),
        ('E', 'F'),
        }
find(fields, custom)

翻译模块之数据结构

但是上面的算法中，自定义翻译的存储方式比较浪费空间，('A', 'B')和 ('A', 'B', 'C') 里的 A, B 重复存储了，而且查找操作也比较低效，这里自然想到用树来保存自定义翻译。同时在实际场景中，为了实现共享翻译功能，选择基于图构建表结构以及字段之间的关系。

一开始会读取表结构以及翻译数据在内存中构建对应的翻译图，最后数据结构如图所示：

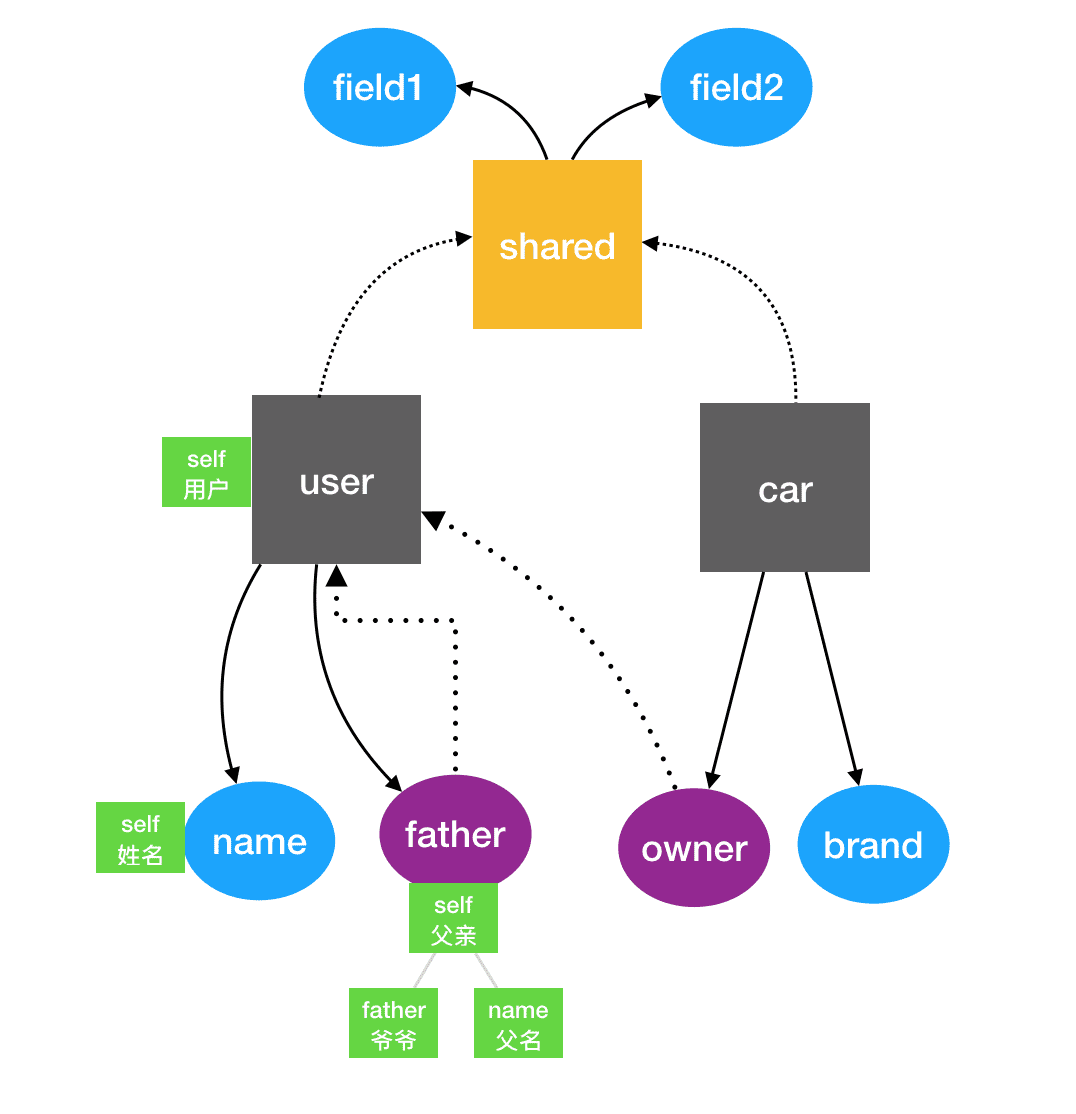
• 正方形代表图中的表节点
  • 黑色表示常规表节点
  • 黄色表示共享翻译节点
• 椭圆形表示图中的字段节点
  • 蓝色为普通字段
  • 紫色为外键字段
• 绿色矩形为翻译树的节点

结果

上线后结果不错，性能大幅提升，翻译速度从原来的平均每次 1ms，下降到 10us 级别，而内存因为使用图避免了很多不必要的重复创建，下降为原来的四分之一。

尾声

平常更多的是处理业务问题，最常用算法的地方就是在 LeetCode 了，难得在实际场景中应用一番，而且体验还不错，希望之后在实践中能遇到更多有意思的算法问题。